이분 탐색

이번에는 이분 탐색에 대해서 정리해볼 것이다.

이분탐색이란?

• 정렬되어 있는 배열에서 특정한 값을 찾아내는 알고리즘이다.
• 배열에서 중간 값을 선택하여 찾는 값과 비교하고, 중간 값이 찾는 값 보다 작다면 우측을 대상으로 찾는 값 보다 크다면 좌측을 대상으로 탐색을 진행해나가며 탐색범위를 반씩 줄여나가는 탐색 방식이다.
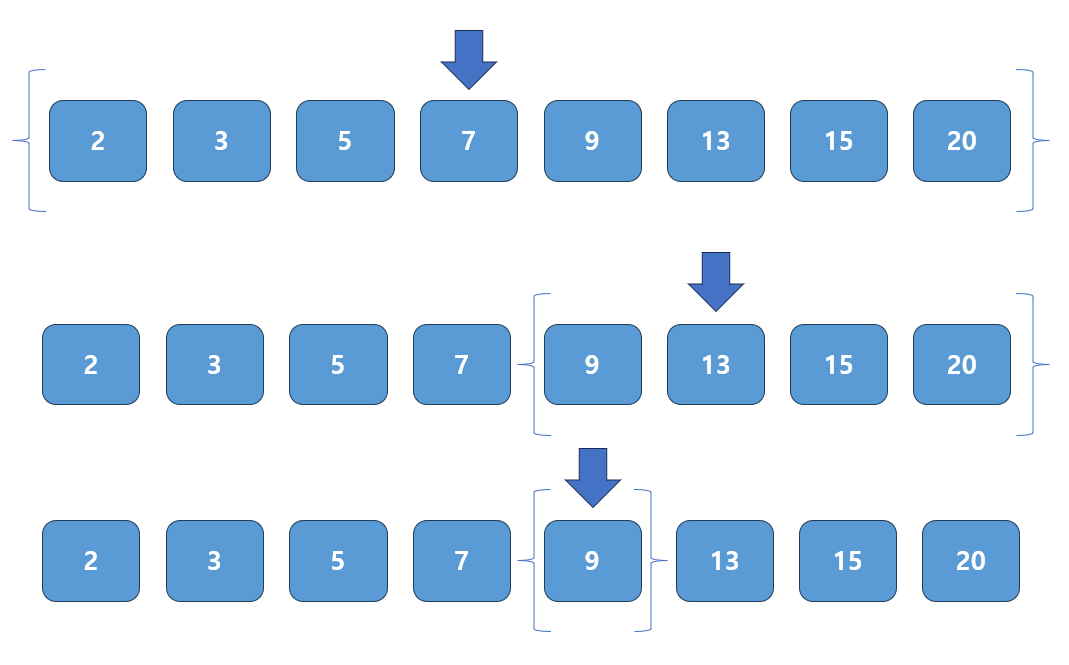
• 예를 들어 살펴보자. ( 2 3 5 7 9 13 15 20, 찾는 값 = 9 )
  • 1회차
    • 2 3 5 7 9 13 15 20
    • 가운데 값인 7을 선택하여 찾는 값인 9와 비교한다.
    • 중간 값이 더 작기 때문에 우측을 기준으로 탐색을 진행한다.
  • 2회차
    • 9 13 15 20
    • 이번에도 역시 가운데 값인 13을 선택해서 찾는 값인 9와 비교한다.
    • 중간 값이 더 크기 때문에 좌측을 기준으로 탐색을 진행한다.
  • 3회차
    • 9
    • 찾는 값인 9와 동일하므로 탐색을 종료한다.

코드 (Java)

int start = 0;
int end = arrLength-1;

Arrays.sort(arr);

while(start <= end) {
    int mid = (int)(end + start)/2;
    if(arr[mid] == target){
        answer = mid + 1;
        break;
    }
    if (arr[mid] > target){
        end = mid - 1;
    }else {
        start = mid + 1;
    }
}

• start와 end로 시작과 끝 인덱스를 지정해둔다.
• mid 를 통해 가운데 값을 얻어오고, 값을 비교해서 때에 알맞은 코드를 실행한다.

시간복잡도

• 이분 탐색에서의 시간복잡도는 O(logN)이다.
• 단계마다 탐색 범위를 반으로 나누어서 비교를 진행하기 때문에 위와 같은 시간 복잡도를 가지게 된다.