이번에는 퀵 정렬에 대해서 정리해보려고한다.
퀵 정렬이란?
퀵 정렬은 불안정 정렬이며, 다른 원소와의 비교만으로 정렬을 수행하는 비교 정렬 방법이다.
- 불안정 정렬?
- 정렬 과정에서 같은 값을 가진 요소의 상대적 순서가 보장되지 않는 정렬을 뜻한다.
- 예를들어,
[a1, b, c, a2]가 있다고 가정하겠다.- a1, a2는 같은 a이며, 위 예제에서는 이해하기 쉽도록 a1, a2로 설명하겠다.
- 정렬이 완료된 후
[a2, a1, b, c]가 될 수도 있고,[a1, a2, b, c]가 될 수도 있다. - 이처럼 정렬 이후 상대적으로 뒤에 있던 a2가 항상 뒤에 오는 것이 아닌 앞으로 올 수도 있기에, 상대적인 순서를 보장하지 못하는 불안정 정렬이라고 불린다.
분할 정복 알고리즘의 하나이며, 배열을 비균등하게 분할하여 정렬을 수행한다.
- 분할 정복 알고리즘?
- 문제를 작은 하위 문제로 나누고, 각 하위 문제들을 해결한 후 그 결과를 결합하여 원래 문제를 해결하는 접근 방식이다.
- 보통 아래와 같은 단계를 거치게 되어있다.
- 분할(Divide): 해결하고자 하는 문제를 더 작은 하위 문제로 분할 한다.
- 정복(Conquer): 각 하위 문제를 재귀적으로 해결한다. 만약 하위 문제를 더 이상 나눌 수 없다면 해결할 수 있다.
- 결합(Combine): 하위 문제의 해를 결합하여 원래 문제의 해를 구한다.
평균적으로 빠른 수행 속도를 보장하기에, 주로 사용하는 곳에서 개선된 방법으로 사용되고 있다.
- 알고리즘을 풀면서 흔히 사용하는
Arrays.sort()는 기본 타입 배열에 대해 듀얼 피벗 퀵정렬을 사용한다. - 객체 배열에 대해서는 팀정렬 알고리즘을 사용한다.
- 팀정렬은 병합 정렬 + 삽입 정렬의 장점만을 결합한 알고리즘으로 안정적인 정렬 방법이다.
본 글에서는 일반적인 퀵 정렬과 듀얼 피벗 퀵정렬에 대해 간단하게 알아볼 것이며, 이외에도 주로 사용하는 정렬 기능의 차이와 어떤 방법을 선택하면 좋을 지에 대해서는 아래 글을 참고하면 좋을 것 같다.
[Java] Java의 정렬 알고리즘 - Arrays와 Collections
동작 과정
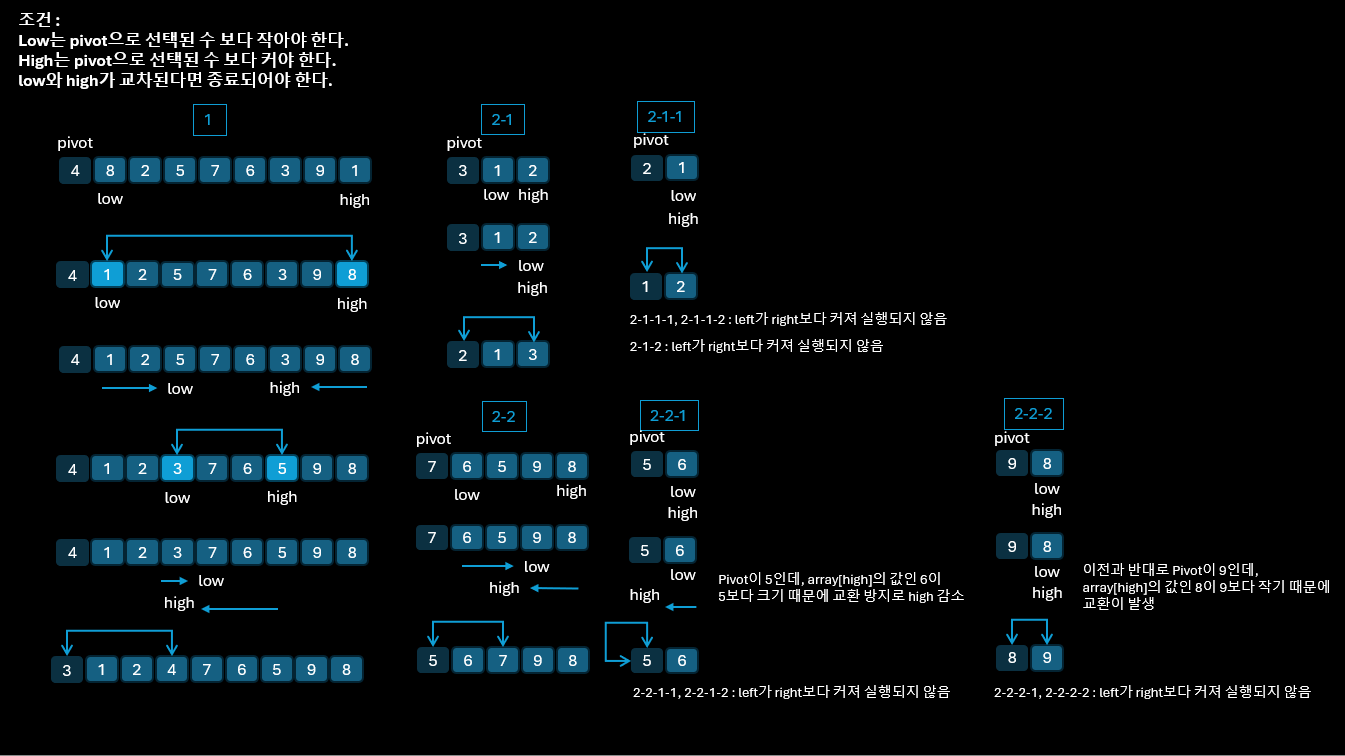
기본적으로 맨 왼쪽 원소를 pivot으로 설정하고, 이를 제외한 맨 왼쪽의 원소를 low, 맨 오른쪽의 원소를 high로 설정한다.
이후 조건에 맞춰 low를 증가시켜주거나, high를 줄여가며 교환하고 마지막에는 pivot과 high의 위치를 교환하게 된다.
pivot을 기준으로array[low]의 값이 작다면 정렬 대상이 아니니low를 증가시킨다.- 반대로
array[low]의 값이 크다면 정렬 대상이 되는 것이다.
- 반대로
pivot을 기준으로array[high]의 값이 크다면 정렬 대상이 아니니high를 감소시킨다.- 반대로
array[high]의 값이 작다면 정렬 대상이 되는 것이다.
- 반대로
pivot을 기준 값으로 정했고, 이를 통해 왼쪽과 오른쪽으로 비교해가며 교환했으니 교차되는 지점에서 pivot과 교환하여 배열을 절반으로 나눌 수 있다.
자료를 기준으로 자세히 살펴보자면 아래와 같다. ( 4, 8, 2, 5, 7, 6, 3, 9, 1 )
- Depth - 1
- 4 8 2 5 7 6 3 9 1 ⇒ 4 1 2 5 7 6 3 9 8 ⇒ 4 1 2 3 7 6 5 9 8 ⇒ 3 1 2 4 7 6 5 9 8
- pivot : 4 / left : 0, right : 8
- low : 1, high : 8
- 왼쪽 - array[1]인 8은 4보다 크기 때문에 정렬 대상이다.
- 오른쪽 - array[8]인 1은 4보다 작기 때문에 정렬 대상이다.
- low : 3, high : 6
- 왼쪽 - array[3]인 5는 4보다 크기 때문에 정렬 대상이다.
- 오른쪽 - array[6]인 3은 4보다 작기 때문에 정렬 대상이다.
- low : 4, high : 3
- low와 high가 교차되었음을 확인하고 교환을 종료하며, 교차된 지점과 pivot을 교환한다.
- low : 1, high : 8
- pivot : 4 / left : 0, right : 8
- 4 8 2 5 7 6 3 9 1 ⇒ 4 1 2 5 7 6 3 9 8 ⇒ 4 1 2 3 7 6 5 9 8 ⇒ 3 1 2 4 7 6 5 9 8
- Depth - 2
- 3 1 2 4 7 6 5 9 8
- 이전 pivot값인 4를 기준으로 왼쪽 배열, 오른쪽 배열로 나눈다.
- 3 1 2 ⇒ 2 1 3
- pivot : 3 / left : 0, right : 3
- low : 2, high : 2
- low와 high가 교차되었음을 확인하고 교환을 종료하며, 교차된 지점과 pivot을 교환한다.
- low : 2, high : 2
- pivot : 3 / left : 0, right : 3
- 7 6 5 9 8 ⇒ 5 6 7 9 8
- pivot : 7 / left : 4, right : 8
- low : 7, high : 6
- low와 high가 교차되었음을 확인하고 교환을 종료하며, 교차된 지점과 pivot을 교환한다.
- low : 7, high : 6
- pivot : 7 / left : 4, right : 8
- 3 1 2 ⇒ 2 1 3
- 이전 pivot값인 4를 기준으로 왼쪽 배열, 오른쪽 배열로 나눈다.
- 3 1 2 4 7 6 5 9 8
- Depth - 3
- 2 1 3 4 5 6 7 9 8
- 2 1 3
- 이전 pivot 값인 3을 기준으로 왼쪽 배열, 오른쪽 배열로 나눈다.
- 2 1 ⇒ 1 2
- pivot : 2 / left : 0, right : 1
- low : 1, high : 1
- low와 high가 교차되었음을 확인하고 교환을 종료하며, 교차된 지점과 pivot을 교환한다.
- low : 1, high : 1
- pivot : 2 / left : 0, right : 1
- 오른쪽 배열 없음
- 2 1 ⇒ 1 2
- 이전 pivot 값인 3을 기준으로 왼쪽 배열, 오른쪽 배열로 나눈다.
- 5 6 7 9 8
- 이전 pivot 값인 7을 기준으로 왼쪽 배열, 오른쪽 배열로 나눈다.
- 5 6 ⇒ 5 6
- pivot : 5 / left : 4, right : 5
- low : 5, high : 5
- Pivot이 5인데, array[high]의 값인 6이 5보다 크기 때문에 교환 방지로 high 감소
- low : 5, high 4
- low와 high가 교차되었음을 확인하고 교환을 종료하며, 교차된 지점과 pivot을 교환한다.
- low : 5, high : 5
- pivot : 5 / left : 4, right : 5
- 9 8 ⇒ 8 9
- pivot : 9 / left : 7, right : 8
- low : 8, right : 8
- low와 high가 교차되었음을 확인하고 교환을 종료하며, 교차된 지점과 pivot을 교환한다.
- 위와 반대로 Pivot이 9인데, array[high]의 값인 8이 9보다 작기 때문에 교환이 발생
- low : 8, right : 8
- pivot : 9 / left : 7, right : 8
- 5 6 ⇒ 5 6
- 이전 pivot 값인 7을 기준으로 왼쪽 배열, 오른쪽 배열로 나눈다.
- 2 1 3
- 2 1 3 4 5 6 7 9 8
- 각 하위 배열의 정렬 결과를 조합하면 아래와 같다.
- 1 2 3 4 5 6 7 8 9
구현
사진이나 글만 보면 이해하기 어려울 수 있다.
아래 코드를 첨부하니 디버깅과 같이 살펴보거나 코드와 같이 위 내용을 읽어보면 이해하기 쉬울 것이다.
코드 (Java)
private void quickSort(int[] array, int left, int right) {
if (left < right) {
int partitioned = partition(array, left, right);
quickSort(array, left, partitioned-1);
quickSort(array, partitioned+1, right);
}
}
private int partition(int[] array, int left, int right) {
int low = left+1;
int high = right;
int pivot = array[left];
while (low <= high) {
while (low < right && array[low] < pivot) {
low++;
}
while (high > left && array[high] > pivot) {
high--;
}
if (low<high) {
int tmp = array[low];
array[low] = array[high];
array[high] = tmp;
}else {
break;
}
}
int tmp = array[left];
array[left] = array[high];
array[high] = tmp;
return high;
}시간복잡도
퀵 정렬은 아래와 같은 시간 복잡도를 가지고 있다.
- 최선의 경우 : O(n log n)
- 평균 : O(n log n)
- 평균적으로 O(n log n)의 시간복잡도를 가지는 힙 정렬, 병합 정렬 중에서도 가장 빠르다.
- 이는 자리가 고정된 pivot이 연산에서 제외되며, 불필요한 데이터의 이동을 줄이고 먼 거리의 데이터끼리 교환하는 특성을 가지고 있기 때문이다.
- 최악의 경우 : O(n^2)
- 특히 이미 정렬된 배열에 대한 정렬을 시도할 경우 최악의 상황을 야기 할 수 있음을 주의하자.
부록 - 듀얼 피봇 퀵정렬
듀얼 피봇 퀵정렬은 일반적인 퀵정렬을 좀 더 개선한 알고리즘이다.
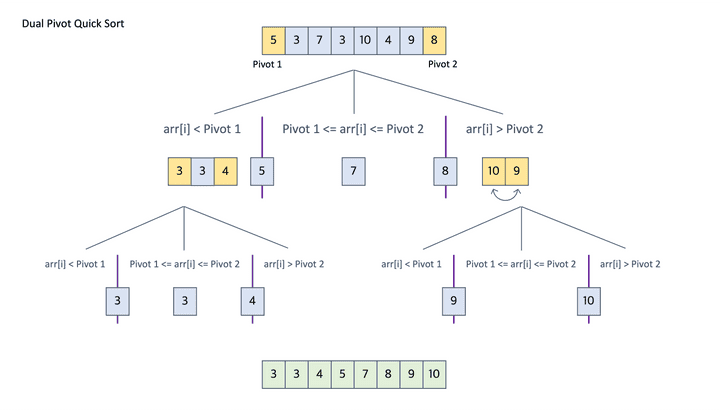
이름에서 부터 알 수 있다시피 두 개의 pivot을 정하고 배열을 3개로 나누는 방법이다.
일반적으로 양쪽 끝의 원소를 pivot으로 사용하며 나머지 부분은 퀵 정렬과 동일하게 동작한다.
성능이 좀 더 좋아질 수는 있지만, 구현이 더 복잡하고, 시간 복잡도 또한 동일하다고 봐도 무방하다.
참고
'알고리즘' 카테고리의 다른 글
| 플로이드 워셜 (Floyd-Warshall) (with. 백준 11404) (4) | 2024.09.08 |
|---|---|
| DFS와 BFS (+인접 행렬과 인접 리스트 / with. 백준 1260) (0) | 2024.09.02 |
| 투 포인터 (0) | 2023.07.26 |
| 이분 탐색 (0) | 2023.07.25 |
| 삽입 정렬 (1) | 2023.07.25 |
