Notion - 위상 정렬 (Topology Sort)
이번에는 위상 정렬에 대해 정리하고, 문제를 기준으로 이해해보자!
https://www.acmicpc.net/problem/2252 - 줄 세우기 / Gold 3
위 문제의 예제인 아래 입력을 기준으로 설명해보도록 하겠다.
4 2
4 2
3 1위상 정렬, Topology Sort?
위상 정렬은 뱡향이 정해져 있는 그래프에서 순서대로 정렬하기 위해 사용되는 알고리즘이다.
특히 이 알고리즘은 방향이 있으며 순환하지 않는 그래프, DAG(Directed Acyclic Graph)에만 적용이 가능하다는 조건이 붙는다.
위상 정렬을 구현하기 전에 이해해야 할 두 가지 개념을 이해해두면 도움이 될 것이다.
진입차수 (in-degree, 입력차수)
- 어떤 노드 N으로 향하는 간선의 개수
진출차수 (out-degree, 출력차수)
- 어떤 노드 N에서 다른 노드로 향하는 간선의 개수
위 문제의 입력이 들어왔을 때, 아래와 같이 유향 그래프가 만들어지는데, 이 때의 진입차수와 진출차수를 구해보면 아래와 같다.

위상 정렬에서는 보통 진입차수와 큐를 이용한 구현을 많이 이용한다.
이를 Khan 알고리즘이라고도 부르며 이외에도 DFS로도 구현이 가능하다.
아래는 Khan 알고리즘을 기준으로 설명했으며, 큐에서 나오는 순서가 위상 정렬된 순서임을 기억하면 된다.
먼저, 진입차수가 0인 노드를 모두 큐에 담아준다.
- 3, 4 가 큐에 담아진다.

큐에서 노드를 하나씩 꺼내며 인접리스트를 탐색하여 이동할 수 있는 노드들에 대한 진입차수를 감소 시키고, 진입차수가 0이 되었다면 큐에 담는다. (설명의 편의상 3과 4의 경우를 한꺼번에 진행함)
- 3의 경우는 1의 진입차수 감소 ⇒ 1의 진입차수가 0이 됨
- 4의 경우는 2의 진입차수 감소 ⇒ 2의 진입차수가 0이 됨
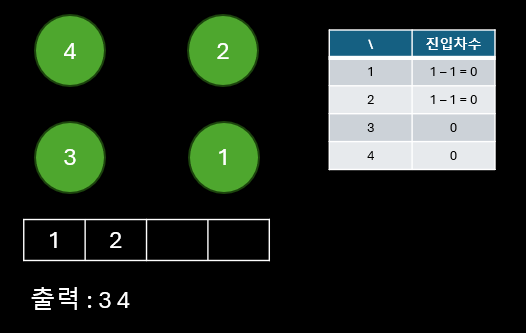
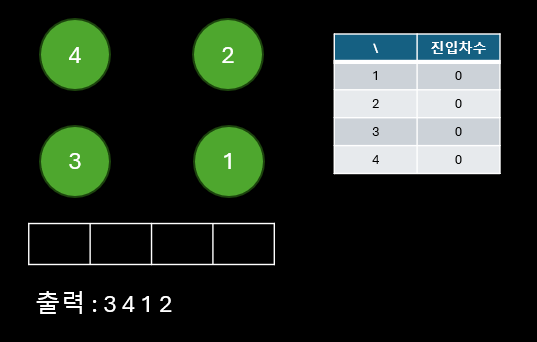
나머지 노드도 위와 같은 방법으로 큐에서 꺼내며 순서를 등록해준다.
구현 - Khan 알고리즘
private static void topologicalSort(){
Queue<Integer> queue = new LinkedList<>();
for (int i = N; i >= 1; i--) {
if(indegree[i] == 0) { // 해당 노드로의 방향이 더 이상 없을 경우에 큐에 추가
queue.offer(i); // 해당 노드를 이용했다는 개념으로 큐에 추가한다고 생각하면 됨
}
}
for (int i = 0; i < N; i++) {
if (!queue.isEmpty()) {
int node = queue.poll();
answer.append(node).append(" "); // 간선이 더 이상 없는 경우, 순서가 정해진 것이기에, StringBuffer에 추가
for (int j = 0; j < list.get(node).size(); j++) { // 인접리스트 탐색
int index = list.get(node).get(j);
indegree[index]--; // 해당 노드에서 갈 수 있는 방향의 진입차수 감소 (= 간선 사용)
if (indegree[index] == 0) { // 간선을 타고 이동했을 때, 만약 더 이상 해당 노드로 접근할 타 노드가 없을 경우
queue.offer(list.get(node).get(j)); // 해당 노드를 완료 처리하기 위해 큐에 추가
}
}
}
}
}위에서 언급한 것 처럼 Khan 알고리즘은 진입차수를 중심으로 문제를 해결해나간다.
- 진입차수가 0인 노드를 모두 찾아 큐에 넣는다.
- 큐의 최상단 노드를 뽑아 해당 노드가 가리키는 모든 노드의 진입차수를 1 감소시킨다.
- 만약 그 과정에서 진입 차수가 0이 된 경우가 있다면 마찬가지로 큐에 넣는다.
- 큐가 빌 때 까지 위 동작을 반복한다.
위 과정에서 큐에서 빠져나간 순서가 바로 위상 정렬된 순서이다.
본 문제에는 “답이 여러 가지인 경우에는 아무거나 출력한다.” 라는 전제조건이 있기에 테스트 케이스 상 정답은 4 2 3 1이라 적혀있으나, 4가 2보다 앞에있고, 3이 1보다 앞에 있음을 만족하면 정답으로 처리된다.
위 코드는 실제로 3 4 1 2 로 출력되지만 정답으로 처리됬으며, 단순하게 큐에 담는 순서나 출력 단을 수정해주면 4 2 3 1로도 출력할 수 있다.
궁금하다면 관련 내용은 전체코드의 주석을 참고하길 바란다.
구현 - DFS
private static void topologicalSort_DFS() {
visited = new boolean[N + 1];
stack = new Stack<>();
for (int n = 1; n <= N; n++) {
if(visited[n]) continue;
dfs(n);
}
}
private static void dfs(int node) {
visited[node] = true;
for(int next : list.get(node)) {
if(visited[next]) continue;
dfs(next);
}
stack.add(node);
}DFS를 통한 구현은 위와 같이 이루어진다.
- 방문 처리를 위한 visited 배열과 정렬된 노드를 담기 위한 stack을 준비한다.
- 방문하지 않은 노드를 찾고, 인접리스트를 통해 다른 노드로 이동할 수 있는 길을 찾는다.
- 방문할 노드가 없다면 방문 완료 처리를 위해 스택에 저장한다.
위와 같은 과정으로 1 → 2 → 3 → 4 순으로 스택에 담기게 되고, 4 3 2 1 로 출력된다.
정리 & 추천 문제
위상 정렬은 방향이 정해져 있는 그래프에서 순서를 정렬하기 위해 사용되는 알고리즘이다.
DAG, 유향 그래프이면서 순환하지 않는 구조에서만 적용할 수 있다.
진입 차수와 큐를 이용한 khan 알고리즘이 주로 사용되며, DFS로도 구현할 수 있다.
이번에도 위상정렬을 연습하기 좋은 문제들을 추천할테니 풀어보면서 연습하면 도움이 될 거라고 생각한다.
https://www.acmicpc.net/problem/1005 - ACM Craft / Gold 3
https://www.acmicpc.net/problem/1516 - 게임 개발 / Gold 3
https://www.acmicpc.net/problem/1766 - 문제집 / Gold 2
전체 코드
package BaekJoon.Gold.Pr2252;
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.ArrayList;
import java.util.LinkedList;
import java.util.List;
import java.util.Queue;
import java.util.Stack;
import java.util.StringTokenizer;
public class Pr2252 {
private static List<List<Integer>> list;
private static StringBuffer answer;
private static int N;
private static int[] indegree;
private static boolean[] visited;
private static Stack<Integer> stack;
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
N = Integer.parseInt(st.nextToken());
int M = Integer.parseInt(st.nextToken());
indegree = new int[N+1];
list = new ArrayList<>();
answer = new StringBuffer();
for (int i = 0; i <= N; i++) {
list.add(new ArrayList<>());
}
for (int i = 0; i < M; i++) {
st = new StringTokenizer(br.readLine());
int A = Integer.parseInt(st.nextToken());
int B = Integer.parseInt(st.nextToken());
list.get(A).add(B);
indegree[B]++; // 해당 노드로의 방향이 있는 경우에는 다른 노드에서의 길이 있는 경우이기 때문에 탐색하도록 진입차수 증가
// ex) 1 3 이라면, 1이 3보다 앞에 있어야 함, 이는 1에서 3으로 향하는 간선이 있다는 뜻
}
//위상 정렬
topologicalSort();
//topologicalSort_DFS();
//while(!stack.isEmpty()) {
// answer.append(stack.pop()).append(' ');
//}
System.out.println(answer);
}
private static void topologicalSort(){
Queue<Integer> queue = new LinkedList<>();
for (int i = N; i >= 1; i--) {
if(indegree[i] == 0) { // 해당 노드로의 방향이 더 이상 없을 경우에 큐에 추가
queue.offer(i); // 해당 노드를 이용했다는 개념으로 큐에 추가한다고 생각하면 됨
}
}
for (int i = 0; i < N; i++) {
if (!queue.isEmpty()) {
int node = queue.poll();
answer.append(node).append(" "); // 간선이 더 이상 없는 경우, 순서가 정해진 것이기에, StringBuffer에 추가
for (int j = 0; j < list.get(node).size(); j++) { // 인접리스트 탐색
int index = list.get(node).get(j);
indegree[index]--; // 해당 노드에서 갈 수 있는 방향의 진입차수 감소 (= 간선 사용)
if (indegree[index] == 0) { // 간선을 타고 이동했을 때, 만약 더 이상 해당 노드로 접근할 타 노드가 없을 경우
if (list.get(index).isEmpty()) {
answer.append(index).append(" "); // 간선이 더 이상 없는 경우, 노드를 거쳤음을 표기하기 위해 StringBuffer에 추가
continue;
}
queue.offer(list.get(node).get(j)); // 해당 노드를 완료 했음 처리하기 위해 큐에 추가
}
}
}
}
}
private static void topologicalSort_DFS() {
visited = new boolean[N + 1];
stack = new Stack<>();
for (int n = 1; n <= N; n++) {
if(visited[n]) continue;
dfs(n);
}
}
private static void dfs(int node) {
visited[node] = true;
for(int next : list.get(node)) {
if(visited[next]) continue;
dfs(next);
}
stack.add(node);
}
}
/***
* 위와 같은 방식을 반복하여 순서를 정함
* 4 2
* 3 1
* 이 입력 됬을 경우
*
* 3과 4의 count가 0이다. == 3과 4로 향하는 간선이 없다.
* 3과 4를 완료 처리하고, 인접리스트를 통해 다른 노드로 향하는 간선이 있는지 확인한다.
*
* 3의 경우는 1, 4의 경우는 2로 이동할 수 있다.
* 3을 답에 추가하고 간선을 사용해서 해당 노드로 이동하고 1의 경우는 큐에 추가
* 이어서 4를 답에 추가하고 간선을 사용해서 해당 노드로 이동하고 2의 경우는 큐에 추가
*
* 1과 2는 둘 다 count가 0이 되었으니 답에 순서대로 추가
* 답은 3 4 1 2
*
* 백준 테스트케이스 2번의 답은 4 2 3 1이라고 써있다.
* 이는 "답이 여러 가지인 경우에는 아무거나 출력한다." 라는 전제가 깔려있으며,
* 3 4 1 2 나 4 2 3 1 둘 다 4가 2앞에 있고, 3이 1 앞에 있음을 만족하기 때문에 상관 없는 것이다. (단순 출력단의 차이인 것이다.)
* 실제로 큐에 넣는 순서를 바꾸고, 위 조건문을 추가하면 4 2 3 1로 출력되며 이 또한 정답임을 볼 수 있다.
*/참고
25. 위상 정렬(Topology Sort)
위상 정렬(Topology Sort)은 '순서가 정해져있는 작업'을 차례로 수행해야 할 때 그 순서를 ...
blog.naver.com
'알고리즘' 카테고리의 다른 글
| 동적계획법 (Dynamic Programming; DP) (with. 백준 1912) (2) | 2024.09.27 |
|---|---|
| 다익스트라 (Dikjstra) (with. 백준 1916) (1) | 2024.09.14 |
| 플로이드 워셜 (Floyd-Warshall) (with. 백준 11404) (4) | 2024.09.08 |
| DFS와 BFS (+인접 행렬과 인접 리스트 / with. 백준 1260) (0) | 2024.09.02 |
| 퀵 정렬 (0) | 2024.05.27 |
