이번에는 플로이드 워셜에 대해서 정리하고, 문제를 기준으로 이해해보자.
https://www.acmicpc.net/problem/11404 - 플로이드 / Gold 4
위 문제의 예제인 아래 입력을 기준으로 설명해보도록 하겠다.
5
14
1 2 2
1 3 3
1 4 1
1 5 10
2 4 2
3 4 1
3 5 1
4 5 3
3 5 10
3 1 8
1 4 2
5 1 7
3 4 2
5 2 4플로이드 워셜 알고리즘?
플로이드 워셜은 모든 노드 간의 최단경로를 구할 때 사용되는 알고리즘이다.
플로이드 워셜 3중 for문을 이용해서 구현할 수 있다.
우선 예제를 기준으로 표현해보자면 아래와 같다.
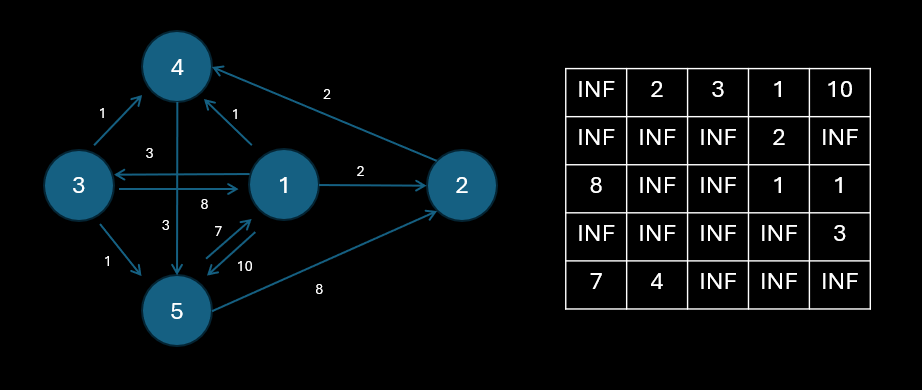
예제에서 나온 중복되는 경로에서의 큰 값은 제외하고 인접행렬을 만들었을 때 오른쪽과 같이 만들어 낼 수 있다.
여기서 INF는 Infinity의 줄임말로 해당 노드로 이동할 수 있는 방법이 없음을 표현한 것이다.
플로이드 워셜 알고리즘은 위와 같은 상황에서 다른 노드를 통해 해당 노드로 접근하는 경로를 찾아낼 수 있다.
구현
위에서 언급 했던 것 처럼 플로이드 워셜 알고리즘은 3중 for문을 이용한다.
private static void floydWarshall() {
for (int i = 1; i <= N; i++) { // 중간
for (int j = 1; j <= N; j++) { // 처음
for (int k = 1; k <= N; k++) { // 끝
if (j == k) continue;
if (graph[j][k] > graph[j][i] + graph[i][k]) {
graph[j][k] = graph[j][i] + graph[i][k];
}
}
}
}
}각 for문의 역할은 중간 노드, 처음 노드, 끝 노드를 맡게 되며 중점적으로 봐야할 내용은 “처음 노드에서 끝 노드로 가야할 때 중간 노드를 거쳐서 가는게 더 빠른가?” 이다.
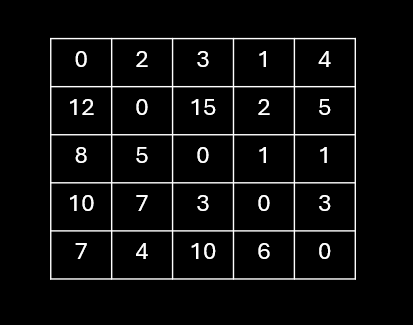
예를 들어 위 그림에서는 끊겨서 갈 수 없어 보이는 2번에서 3번 노드로 방문하는 것을 살펴보자.
2 → 4 → 5 → 1 → 3 순서를 따라 총 15의 가중치를 통해 2번 노드를 방문 할 수 있다.
3중 for문을 통해 아래와 같이 두 경로가 탐색되고 이동이 가능하게 된다.
- 5 → 1 → 3 : 10
- 2 → 4 → 5 : 5
- 2 → 5 → 3 : 15
본래 5 → 3의 경로는 없기에 INF라는 가중치를 갖고 있지만, 5 → 1 → 3의 경로는 10이라는 가중치로 이동할 수 있으므로 5 → 3의 INF를 10으로 대체한다.
마찬가지로 2 → 5의 경로는 INF라는 가중치를 갖고 있지만, 2 → 4 → 5의 경로는 5라는 가중치로 이동할 수 있으므로 2 → 5의 INF를 5로 대체한다.
마지막에도 동일하게 2 → 3의 경로는 INF라는 가중치를 갖고 있지만, 2 → 5 → 3의 경로는 15라는 가중치로 이동할 수 있으므로 2 → 3의 INF를 15로 대체한다.
위와 같은 식으로 모든 경로의 대한 가중치가 중간 노드를 거쳐서 가는게 더 빠른지를 검사하여 대체하다보면 아래와 같은 인접 행렬을 완성할 수 있다.
정리 & 추천 문제
플로이드 워셜은 모든 노드 간의 최단경로를 구할 때 사용되는 알고리즘이다.
3중 for문을 이용해서 구현할 수 있어 구현이 쉽지만, 변형 문제들은 약간의 생각을 가미해야 한다.
처음 노드에서 끝 노드로 가야할 때 중간 노드를 거쳐서 가는게 더 빠른가? 만 고려한다면 플로이드 워셜 알고리즘을 활용한 문제를 풀어낼 수 있다고 생각한다.
아래는 추가로 풀어보기 좋은 플로이드 워셜 문제들을 첨부한다.
https://www.acmicpc.net/problem/1389 - 케빈 베이컨의 6단계 법칙 / Silver 1
https://www.acmicpc.net/problem/2458 - 키 순서 / Gold 4
전체 코드
package BaekJoon.Gold.Pr11404;
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.StringTokenizer;
public class Pr11404 {
private static int[][] graph;
private static int N, M;
static final int INF = 9999999;
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st;
N = Integer.parseInt(br.readLine());
M = Integer.parseInt(br.readLine());
graph = new int[N+1][N+1];
for (int i = 1; i <= N; i++) {
for (int j = 1; j <= N; j++) {
graph[i][j] = INF;
}
}
for (int i = 0; i < M; i++) {
st = new StringTokenizer(br.readLine(), " ");
int a = Integer.parseInt(st.nextToken());
int b = Integer.parseInt(st.nextToken());
int c = Integer.parseInt(st.nextToken());
graph[a][b] = Math.min(graph[a][b], c);
}
floydWarshall();
for (int i = 1; i <= N; i++) {
for (int j = 1; j <= N; j++) {
if (graph[i][j] == INF) {
System.out.print(0 + " ");
} else {
System.out.print(graph[i][j] + " ");
}
}
System.out.println();
}
}
private static void floydWarshall() {
for (int i = 1; i <= N; i++) { // 중간
for (int j = 1; j <= N; j++) { // 처음
for (int k = 1; k <= N; k++) { // 끝
if (j == k) continue;
if (graph[j][k] > graph[j][i] + graph[i][k]) {
graph[j][k] = graph[j][i] + graph[i][k];
}
}
}
}
}
}
'알고리즘' 카테고리의 다른 글
| 동적계획법 (Dynamic Programming; DP) (with. 백준 1912) (2) | 2024.09.27 |
|---|---|
| 다익스트라 (Dikjstra) (with. 백준 1916) (1) | 2024.09.14 |
| DFS와 BFS (+인접 행렬과 인접 리스트 / with. 백준 1260) (0) | 2024.09.02 |
| 퀵 정렬 (0) | 2024.05.27 |
| 투 포인터 (0) | 2023.07.26 |
