DFS와 BFS에 대해서와 인접 행렬과 인접 그래프에 대해서 정리하고, 한 문제를 통해서 이해해보자.
설명에 앞서 코드에 대한 기준을 정하고 시작하면 좋을 것 같아 아래 문제를 기준으로 설명하도록 하겠다.
https://www.acmicpc.net/problem/1260 - DFS와 BFS / Silver 2
위 문제의 예제 1번인 아래 입력을 기준으로 설명하도록 하겠다.
4 5 1
1 2
1 3
1 4
2 4
3 4DFS (Depth-First Search)
DFS는 깊이 우선 탐색이라고 부르며, 깊은 부분부터 우선적으로 탐색하는 알고리즘이다.
DFS는 Stack 자료구조 혹은 재귀 함수를 이용하여 구현할 수 있다.
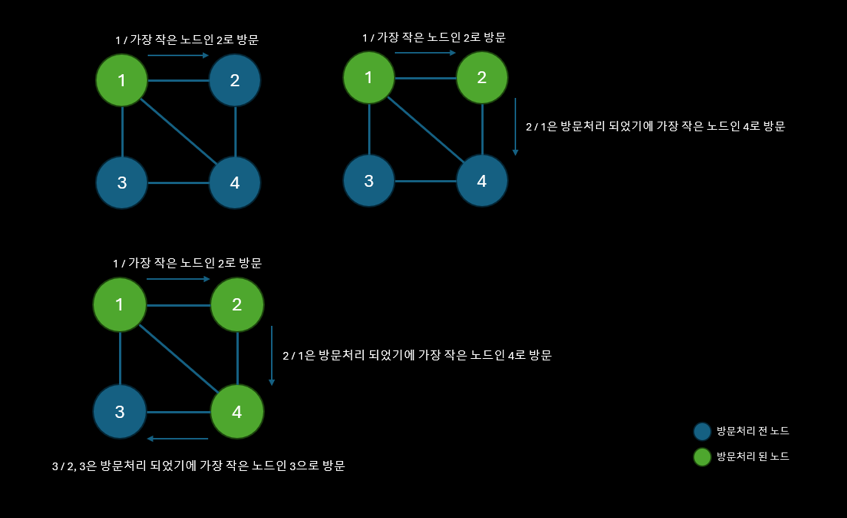
DFS로 위 예제를 탐색하게 되면 1 2 4 3 이라는 결과를 얻을 수 있다.
해당 노드에서 갈 수 있는 방향을 기준으로 가장 작은 노드를 선택해서 방문 처리하며 진행한다.
이를 반복하여 끝까지 도달한다.
구현
Stack
private static void DFS_Stack(int start) {
Stack <Integer> stack = new Stack();
stack.add(start);
while(!stack.isEmpty()) {
int node = stack.pop();
if (!visited[node]) {
System.out.print(node + " ");
visited[node] = true;
}
for (int next : adjList.get(node)) {
if (visited[next]) continue;
stack.add(next);
}
}
}- 탐색 시작 노드를 스택에 삽입하고 아직 방문하지 않은 인접 노드를 탐색하여 스택에 추가한다.
- 스택 내 최상단 노드를 꺼내 아직 방문하지 않은 인접 노드가 있다면 해당 노드를 스택에 넣고 방문 처리를 한다.
- 인접한 노드가 하나도 없으면, 스택에서 최상단 노드를 꺼낸다.
- 2, 3번 과정을 반복한다.
Recursion
private static void DFS_Recursion(int v) {
if (!visited[v]) {
System.out.print(v + " ");
visited[v] = true;
}
for (int i = 0; i < adjList.get(v).size(); i++) {
if (visited[adjList.get(v).get(i)]) continue;
DFS_Recursion(adjList.get(v).get(i));
}
}- 탐색 시작 노드를 메서드의 파라미터에 삽입하고 방문처리를 한다.
- 아직 방문하지 않은 인접 노드가 있다면 해당 노드를 스택프레임에 넣고 방문 처리를 한다.
- 인접한 노드가 하나도 없으면, 스택프레임에서 최상단 노드를 꺼낸다.
- 2, 3번 과정을 반복한다.
BFS (Breadth-First Search)
BFS는 넓이 우선 탐색이라고 부르며, 가까운 노드 부터 우선적으로 탐색하는 알고리즘이다.
BFS는 Queue 자료구조를 이용하여 구현할 수 있다.
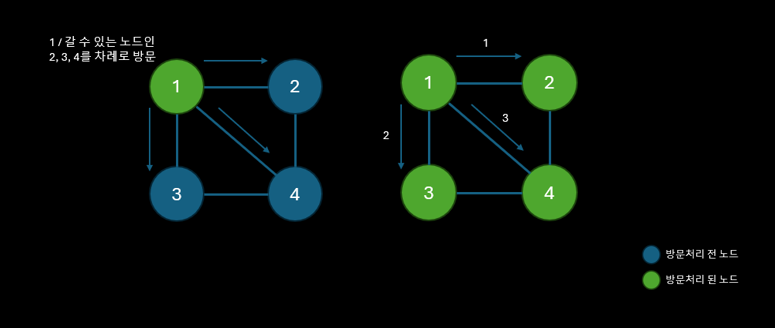
BFS로 위 예제를 탐색하게 되면 1 2 3 4 이라는 결과를 얻을 수 있다.
상위 노드에서 방문 할 수 있는 하위 노드를 모두 큐에 넣고 방문처리를 하며 진행한다.
이를 반복하여 끝까지 도달한다.
구현
Queue
private static void BFS(int root) {
Queue<Integer> queue = new LinkedList<>();
queue.add(root);
visited[root] = true;
while (!queue.isEmpty()) {
int node = queue.poll();
System.out.print(node+" ");
for (int i = 0; i < adjList.get(node).size(); i++) {
if (visited[adjList.get(node).get(i)]) continue;
queue.add(adjList.get(node).get(i));
visited[adjList.get(node).get(i)] = true;
}
}
}- 탐색 시작 노드를 큐에 삽입하고 방문처리를 한다.
- 큐에서 노드를 꺼낸 뒤에 해당 노드의 인접 노드 중에서 방문하지 않은 노드를 모두 큐에 삽입하고 방문 처리를 한다.
- 2번의 과정을 수행할 수 없을 때 까지 반복한다.
인접 행렬과 인접 리스트
사실위에서 소개한 DFS와 BFS는 인접 리스트를 이용한 예제만 적혀있다.
흔히 들어봤던 인접 행렬과 인접 리스트에 대해서 간단하게 알아보고 코드를 살펴보자.
인접 행렬
인접 행렬은 각 노드 간의 관계를 2차원 배열로 풀어내는 방식이다.
노드의 지점을 인덱스 삼아 해당 노드로 이동할 수 있는지 판단할 수 있다.
아래에서는 (1, 2), (1, 3), (1, 4)이 모두 1로 이동할 수 있음을 표시하고 있다.
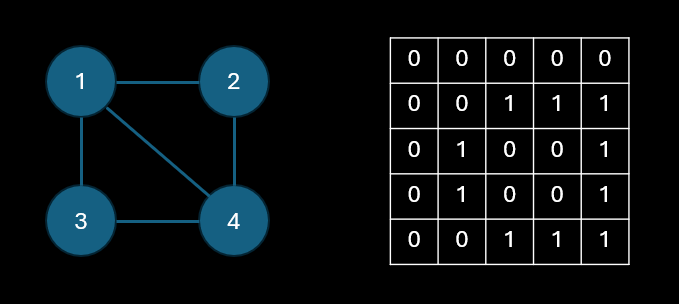
이는 구현이 매우 간단하고 특정 노드의 정보를 확인해야 할 때 매우 빠르게 확인이 가능하다는 장점을 가지고 있다.
위 문제를 인접행렬을 이용해 풀었을 때는 아래와 같다.
private static void DFS_Recursion_AdjArray(int v) {
if (!visited[v]) {
System.out.print(v + " ");
visited[v] = true;
}
for (int i = 0; i < adjArray[v].length; i++) {
if (!visited[i] && adjArray[v][i] == 1) {
DFS_Recursion(adjArray[v][i]);
}
}
}
private static void BFS_AdjArray(int root) {
Queue<Integer> queue = new LinkedList<>();
queue.add(root);
visited[root] = true;
while (!queue.isEmpty()) {
int node = queue.poll();
System.out.print(node+" ");
for (int i = 0; i < adjArray[node].length; i++) {
if (!visited[i] && adjArray[node][i] == 1) {
queue.add(i);
visited[i] = true;
}
}
}
}인접 리스트
인접 리스트는 각 노드 간의 관계를 리스트 형태로 풀어내는 방식이다.
1번 노드의 경우 2, 3, 4번 노드로 이동할 수 있고, 2번은 1, 4번 그리고 3번도 1, 4번 마지막으로 4번은 1, 2, 3번 노드로 이동할 수 있다.
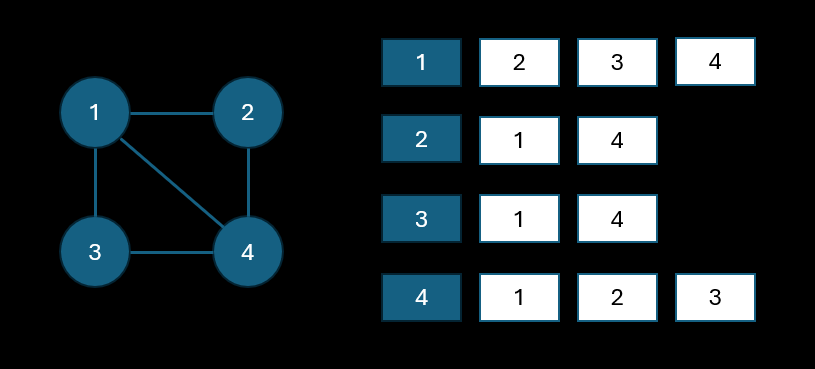
이는 실제로 연결된 노드들의 정보만 기록하기 때문에 간선에 비례한 메모리만 사용할 수 있다는 장점이 있다.
하지만 특정 노드간의 연결 정보를 찾기 위해서는 해당 노드의 정보를 모두 탐색해야하기 때문에 시간이 오래걸릴 수도 있다.
정리
DFS와 BFS는 수많은 그래프 문제의 기초가 되는 탐색법이다.
DFS는 스택 혹은 재귀를 통해 구현하며, BFS는 큐를 통해 구현할 수 있다.
백트래킹, 위상 정렬, 다익스트라 등 앞으로 풀어나갈 고급 알고리즘에 적용시킬 수 있으므로 잘 알아두고 활용하는 것이 중요하다고 생각한다.
인접 행렬과 인접 리스트는 그래프를 표현하는 두 가지 방법이다.
DFS와 BFS는 인접 행렬이나 인접 리스트를 사용하여 그래프를 탐색할 수 있다.
전체 코드
package BaekJoon.Silver.Pr1260;
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.ArrayList;
import java.util.Collections;
import java.util.LinkedList;
import java.util.Queue;
import java.util.Stack;
import java.util.StringTokenizer;
public class Pr1260_Sol {
private static int N, M, V;
private static int[][] adjArray;
private static ArrayList<ArrayList<Integer>> adjList;
private static boolean[] visited;
// 재귀 사용
private static void DFS_Recursion(int v) {
if (!visited[v]) {
System.out.print(v + " ");
visited[v] = true;
}
for (int i = 0; i < adjList.get(v).size(); i++) {
if (visited[adjList.get(v).get(i)]) continue;
DFS_Recursion(adjList.get(v).get(i));
}
}
private static void DFS_Recursion_AdjArray(int v) {
if (!visited[v]) {
System.out.print(v + " ");
visited[v] = true;
}
for (int i = 0; i < adjArray[v].length; i++) {
if (!visited[i] && adjArray[v][i] == 1) {
DFS_Recursion(adjArray[v][i]);
}
}
}
// 스택 사용
private static void DFS_Stack(int start) {
Stack <Integer> stack = new Stack();
stack.add(start);
while(!stack.isEmpty()) {
int node = stack.pop();
if (!visited[node]) {
System.out.print(node + " ");
visited[node] = true;
}
for (int next : adjList.get(node)) {
if (visited[next]) continue;
stack.add(next);
}
}
}
private static void BFS(int root) {
Queue<Integer> queue = new LinkedList<>();
queue.add(root);
visited[root] = true;
while (!queue.isEmpty()) {
int node = queue.poll();
System.out.print(node+" ");
for (int i = 0; i < adjList.get(node).size(); i++) {
if (visited[adjList.get(node).get(i)]) continue;
queue.add(adjList.get(node).get(i));
visited[adjList.get(node).get(i)] = true;
}
}
}
private static void BFS_AdjArray(int root) {
Queue<Integer> queue = new LinkedList<>();
queue.add(root);
visited[root] = true;
while (!queue.isEmpty()) {
int node = queue.poll();
System.out.print(node+" ");
for (int i = 0; i < adjArray[node].length; i++) {
if (!visited[i] && adjArray[node][i] == 1) {
queue.add(i);
visited[i] = true;
}
}
}
}
public static void main(String[] args) throws IOException {
BufferedReader bf = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(bf.readLine());
N = Integer.parseInt(st.nextToken()); // 정점의 개수
M = Integer.parseInt(st.nextToken()); // 간선의 개수
V = Integer.parseInt(st.nextToken()); // 시작할 정점의 번호
// 인접 리스트 초기화
adjList = new ArrayList<>();
for (int i = 0; i < N+1; i++) {
adjList.add(new ArrayList<>());
}
// 인접 행렬 초기화
adjArray = new int[N+1][N+1];
for (int i = 0; i < M; i++) {
st = new StringTokenizer(bf.readLine());
int v1 = Integer.parseInt(st.nextToken());
int v2 = Integer.parseInt(st.nextToken());
adjList.get(v1).add(v2);
adjList.get(v2).add(v1); // 인접 리스트
adjArray[v1][v2] = 1;
adjArray[v2][v1] = 1; // 인접 행렬
}
// 정렬
for (int i = 0; i < N+1; i++) {
Collections.sort(adjList.get(i));
}
// 스택 DFS를 사용 할 경우 내림차순 정렬 필요
// for (int i=0; i<N+1; i++) {
// Collections.sort(adjList.get(i), Collections.reverseOrder());
// }
visited = new boolean[N+1];
DFS_Recursion_AdjArray(V);
System.out.println();
// 이후 다시 오름차순 정렬
// for (int i=0; i<N+1; i++) Collections.sort(graph[i]);
visited = new boolean[N+1];
BFS_AdjArray(V);
}
}
참고
'알고리즘' 카테고리의 다른 글
| 다익스트라 (Dikjstra) (with. 백준 1916) (1) | 2024.09.14 |
|---|---|
| 플로이드 워셜 (Floyd-Warshall) (with. 백준 11404) (4) | 2024.09.08 |
| 퀵 정렬 (0) | 2024.05.27 |
| 투 포인터 (0) | 2023.07.26 |
| 이분 탐색 (0) | 2023.07.25 |
